How To Find Spring Constant From Oscillation

Menses and Frequency

The period is the duration of 1 wheel in a repeating event, while the frequency is the number of cycles per unit time.

Learning Objectives

Do converting between frequency and period

Fundamental Takeaways

Key Points

• Move that repeats itself regularly is called periodic move. One complete repetition of the move is chosen a cycle. The duration of each cycle is the period.
• The frequency refers to the number of cycles completed in an interval of time. It is the reciprocal of the flow and can be calculated with the equation f=1/T.
• Some motility is best characterized by the angular frequency (ω). The angular frequency refers to the angular displacement per unit time and is calculated from the frequency with the equation ω=2πf.

Key Terms

• flow: The duration of one cycle in a repeating outcome.
• angular frequency: The athwart displacement per unit fourth dimension.
• frequency: The quotient of the number of times n a periodic miracle occurs over the time t in which it occurs: f = n / t.

Period and Frequency

The usual physics terminology for motion that repeats itself over and over is periodic motion, and the time required for one repetition is called the menstruation, often expressed as the letter T. (The symbol P is non used because of the possible confusion with momentum. ) Ane complete repetition of the motion is chosen a wheel. The frequency is defined as the number of cycles per unit of measurement time. Frequency is usually denoted by a Latin alphabetic character f or by a Greek letter of the alphabet ν (nu). Note that period and frequency are reciprocals of each other.

Sinusoidal Waves of Varying Frequencies: Sinusoidal waves of various frequencies; the bottom waves have higher frequencies than those above. The horizontal axis represents time.

[latex]\text{f} = 1/\text{T}[/latex]

For example, if a newborn infant's centre beats at a frequency of 120 times a minute, its period (the interval between beats) is half a 2d. If you calibrate your intuition and then that you expect big frequencies to be paired with short periods, and vice versa, yous may avert some embarrassing mistakes on physics exams.

Units

Locomotive Wheels: The locomotive'south wheels spin at a frequency of f cycles per 2d, which tin can also be described every bit ω radians per second. The mechanical linkages allow the linear vibration of the steam engine's pistons, at frequency f, to drive the wheels.

In SI units, the unit of frequency is the hertz (Hz), named after the German language physicist Heinrich Hertz: ane Hz indicates that an event repeats once per second. A traditional unit of measure used with rotating mechanical devices is revolutions per infinitesimal, abbreviated RPM. 60 RPM equals 1 hertz (i.east., one revolution per second, or a period of 1 second). The SI unit of measurement for period is the second.

Angular Frequency

Ofttimes periodic motility is best expressed in terms of angular frequency, represented past the Greek letter ω (omega). Angular frequency refers to the angular deportation per unit of measurement time (eastward.1000., in rotation) or the rate of change of the phase of a sinusoidal waveform (e.thousand., in oscillations and waves), or as the rate of change of the argument of the sine function.

[latex]\text{y}(\text{t}) = \text{sin}(\theta (\text{t}))=\text{sin}(\omega \text{t})=\text{sin}(2\pi \text{ft})[/latex]

[latex]\omega =2\pi \text{f}[/latex]

Angular frequency is ofttimes represented in units of radians per 2nd (recall in that location are 2π radians in a circle).

Period of a Mass on a Spring

The period of a mass grand on a spring of jump abiding 1000 can exist calculated equally [latex]\text{T}=two\pi \sqrt{\frac{\text{m}}{\text{k}}}[/latex].

Learning Objectives

Identify parameters necessary to calculate the period and frequency of an oscillating mass on the end of an platonic spring

Key Takeaways

Fundamental Points

• If an object is vibrating to the correct and left, then information technology must have a leftward force on it when it is on the right side, and a rightward force when information technology is on the left side.
• The restoring forcefulness causes an oscillating object to move back toward its stable equilibrium position, where the net strength on it is zero.
• The simplest oscillations occur when the restoring force is straight proportional to deportation. In this case the force tin be calculated every bit F=-kx, where F is the restoring force, grand is the force constant, and x is the displacement.
• The motion of a mass on a spring can exist described equally Simple Harmonic Motion (SHM): oscillatory motility that follows Hooke's Law.
• The period of a mass on a spring is given past the equation  [latex]\text{T}=ii\pi \sqrt{\frac{\text{thousand}}{\text{k}}}[/latex]

Key Terms

• Restoring force: A variable forcefulness that gives rise to an equilibrium in a concrete system. If the organization is perturbed away from the equilibrium, the restoring strength will tend to bring the system dorsum toward equilibrium. The restoring forcefulness is a role only of position of the mass or particle. It is always directed back toward the equilibrium position of the system
• amplitude: The maximum accented value of some quantity that varies.

Understanding the Restoring Strength

Newton'south outset law implies that an object aquiver dorsum and forth is experiencing forces. Without strength, the object would move in a directly line at a abiding speed rather than oscillate. It is of import to empathise how the force on the object depends on the object's position. If an object is vibrating to the right and left, then it must take a leftward strength on it when information technology is on the right side, and a rightward forcefulness when information technology is on the left side. In i dimension, we tin correspond the direction of the force using a positive or negative sign, and since the force changes from positive to negative in that location must exist a point in the middle where the strength is zero. This is the equilibrium indicate, where the object would stay at balance if it was released at rest. It is mutual convention to define the origin of our coordinate system so that x equals null at equilibrium.

Oscillating Ruler: When displaced from its vertical equilibrium position, this plastic ruler oscillates back and along because of the restoring force opposing displacement. When the ruler is on the left, there is a force to the right, and vice versa.

Consider, for instance, plucking a plastic ruler shown in the first figure. The deformation of the ruler creates a force in the contrary direction, known as a restoring strength. Once released, the restoring force causes the ruler to move back toward its stable equilibrium position, where the net force on it is zero. However, past the time the ruler gets there, it gains momentum and continues to move to the right, producing the reverse deformation. It is then forced to the left, back through equilibrium, and the process is repeated until dissipative forces (due east.g., friction) dampen the movement. These forces remove mechanical energy from the system, gradually reducing the motion until the ruler comes to rest.

Restoring force, momentum, and equilibrium: (a) The plastic ruler has been released, and the restoring force is returning the ruler to its equilibrium position. (b) The net force is zero at the equilibrium position, but the ruler has momentum and continues to move to the right. (c) The restoring force is in the opposite direction. Information technology stops the ruler and moves it back toward equilibrium once more. (d) Now the ruler has momentum to the left. (e) In the absence of damping (acquired by frictional forces), the ruler reaches its original position. From there, the move will echo itself.

Hooke'due south Constabulary

The simplest oscillations occur when the restoring force is directly proportional to displacement. The name that was given to this relationship between strength and displacement is Hooke'southward police force:

[latex]\text{F}=\text{kx}[/latex]

Here, F is the restoring force, x is the deportation from equilibrium or deformation, and 1000 is a abiding related to the difficulty in deforming the organisation (ofttimes called the spring constant or strength constant). Retrieve that the minus sign indicates the restoring force is in the direction contrary to the displacement. The strength constant k is related to the rigidity (or stiffness) of a organisation—the larger the force constant, the greater the restoring force, and the stiffer the system. The units of k are newtons per meter (Northward/m). For example, thou is directly related to Young'due south modulus when we stretch a string. A typical physics laboratory do is to measure restoring forces created by springs, determine if they follow Hooke's law, and calculate their forcefulness constants if they do.

Mass on a Leap

A common instance of an objecting aquiver back and forth according to a restoring forcefulness directly proportional to the displacement from equilibrium (i.eastward., post-obit Hooke'southward Law) is the example of a mass on the end of an ideal spring, where "ideal" means that no messy real-world variables interfere with the imagined outcome.

The movement of a mass on a spring tin be described as Simple Harmonic Move (SHM), the name given to oscillatory motion for a arrangement where the net force tin can exist described by Hooke's law. We tin now determine how to calculate the flow and frequency of an oscillating mass on the stop of an ideal spring. The period T tin be calculated knowing only the mass, 1000, and the force constant, g:

[latex]\text{T}=2\pi \sqrt{\frac{\text{m}}{\text{k}}}[/latex]

When dealing with [latex]\text{f}=i/\text{T}[/latex], the frequency is given past:

[latex]\text{f}=\frac{1}{2\pi} \sqrt{\frac{\text{thousand}}{\text{grand}}}[/latex]

We can understand the dependence of these equations on m and k intuitively. If one were to increment the mass on an oscillating leap organisation with a given grand, the increased mass will provide more than inertia, causing the dispatch due to the restoring force F to decrease (recall Newton's Second Law: [latex]\text{F}=\text{ma}[/latex]). This will lengthen the oscillation catamenia and decrease the frequency. In contrast, increasing the strength constant thou will increase the restoring force co-ordinate to Hooke's Law, in turn causing the acceleration at each displacement indicate to also increase. This reduces the period and increases the frequency. The maximum displacement from equilibrium is known as the amplitude X.

Movement of a mass on an platonic spring: An object attached to a spring sliding on a frictionless surface is an uncomplicated simple harmonic oscillator. When displaced from equilibrium, the object performs simple harmonic motion that has an amplitude X and a menstruum T. The object'due south maximum speed occurs as it passes through equilibrium. The stiffer the bound is, the smaller the menstruum T. The greater the mass of the object is, the greater the catamenia T. (a) The mass has achieved its greatest displacement X to the right and at present the restoring force to the left is at its maximum magnitude. (b) The restoring force has moved the mass back to its equilibrium point and is at present equal to naught, but the leftward velocity is at its maximum. (c) The mass'southward momentum has carried information technology to its maximum displacement to the right. The restoring force is now to the correct, equal in magnitude and opposite in direction compared to (a). (d) The equilibrium point is reach again, this fourth dimension with momentum to the right. (e) The cycle repeats.

Simple Harmonic Movement

Uncomplicated harmonic motion is a blazon of periodic move where the restoring forcefulness is directly proportional to the displacement.

Learning Objectives

Relate the restoring strength and the displacement during the simple harmonic motion

Key Takeaways

Key Points

• Simple harmonic motion is oftentimes modeled with the case of a mass on a spring, where the restoring force obey's Hooke's Law and is directly proportional to the displacement of an object from its equilibrium position.
• Any organization that obeys simple harmonic motility is known as a simple harmonic oscillator.
• The equation of movement that describes elementary harmonic motion can exist obtained by combining Newton's Second Law and Hooke'due south Law into a second-society linear ordinary differential equation: [latex]\text{F}_{\text{net}}=\text{grand}\frac{\text{d}^{2}\text{x}}{\text{dt}^{ii}}=-\text{kx}[/latex].

Fundamental Terms

• unproblematic harmonic oscillator: A device that implements Hooke'south law, such as a mass that is attached to a spring, with the other stop of the bound being connected to a rigid back up, such as a wall.
• oscillator: A pattern that returns to its original land, in the aforementioned orientation and position, afterwards a finite number of generations.

Simple Harmonic Motion

Elementary harmonic move is a type of periodic move where the restoring force is straight proportional to the deportation (i.e., it follows Hooke'due south Law). It can serve as a mathematical model of a variety of motions, such as the oscillation of a jump. In add-on, other phenomena can exist approximated by unproblematic harmonic motility, such as the motility of a simple pendulum, or molecular vibration.

Elementary Harmonic Motion: A brief introduction to simple harmonic motion for calculus-based physics students.

Simple harmonic motion is typified by the motion of a mass on a bound when it is subject to the linear elastic restoring force given by Hooke's Police. A system that follows unproblematic harmonic motion is known as a simple harmonic oscillator.

Dynamics of Elementary Harmonic Oscillation

For one-dimensional simple harmonic motion, the equation of movement (which is a second-order linear ordinary differential equation with abiding coefficients) can exist obtained by means of Newton'due south second law and Hooke's law.

[latex]\text{F}_{\text{internet}}=\text{thousand}\frac{\text{d}^{2}\text{10}}{\text{dt}^{2}}=-\text{kx}[/latex],

where m is the mass of the oscillating trunk, x is its displacement from the equilibrium position, and k is the leap abiding. Therefore:

[latex]\frac{\text{d}^{ii}\text{x}}{\text{dt}^{2}}=-(\frac{\text{k}}{\text{m}})\text{10}[/latex].

Solving the differential equation in a higher place, a solution which is a sinusoidal function is obtained.

[latex]\text{x}(\text{t})=\text{c}_{1}\text{cos}(\omega \text{t})+\text{c}_{two}\text{sin}(\omega \text{t})=\text{Acos}(\omega \text{t} - \varphi )[/latex],

where

[latex]\omega = \sqrt{\frac{\text{k}}{\text{m}}}[/latex],

[latex]\text{A}=\sqrt{\text{c}_{ane}^{two}+\text{c}_{2}^{2}}[/latex],

[latex]tan\varphi=(\frac{\text{c}_{ii}}{\text{c}_{one}})[/latex].

In the solution, c₁ and c₂ are ii constants determined by the initial conditions, and the origin is set to exist the equilibrium position. Each of these constants carries a physical meaning of the movement: A is the aamplitude (maximum deportation from the equilibrium position), ω = 2πf is the angular frequency, and φ is the phase.

We can use differential calculus and find the velocity and acceleration as a part of time:

[latex]\text{v}(\text{t})=\frac{\text{dx}}{\text{dt}}=-\text{A}\omega \text{sin}(\omega \text{t}-\varphi )[/latex]

[latex]\text{a}(\text{t})=\frac{\text{d}^{2}\text{x}}{\text{dt}^{2}}=-\text{A}\omega ^{2}\text{cos}(\omega \text{t}-\varphi )[/latex].

Acceleration can likewise be expressed as a function of displacement:

[latex]\text{a}(\text{t})=-\omega ^{2}\text{10}[/latex].

Then since ω = 2πf,

[latex]\text{f}=\frac{1}{ii\pi }\sqrt{\frac{\text{1000}}{\text{g}}}[/latex].

Recalling that [latex]\text{T}=1/\text{f}[/latex],

[latex]\text{T}=2\pi \sqrt{\frac{\text{thou}}{\text{k}}}[/latex].

Using Newton's 2d Law, Hooke'southward Law, and some differential Calculus, nosotros were able to derive the period and frequency of the mass oscillating on a spring that we encountered in the concluding section! Note that the period and frequency are completely independent of the amplitude.

The below figure shows the simple harmonic motion of an object on a spring and presents graphs of x(t),v(t), and a(t) versus time. Yous should learn to create mental connections between the to a higher place equations, the different positions of the object on a jump in the cartoon, and the associated positions in the graphs of x(t), v(t), and a(t).

Visualizing Uncomplicated Harmonic Motility: Graphs of x(t),v(t), and a(t) versus t for the move of an object on a spring. The net forcefulness on the object can be described past Hooke'south law, then the object undergoes unproblematic harmonic motion. Note that the initial position has the vertical displacement at its maximum value X; v is initially zero and and so negative as the object moves down; and the initial dispatch is negative, back toward the equilibrium position and becoming zero at that point.

Simple Harmonic Move and Uniform Circular Movement

Elementary harmonic motion is produced by the projection of uniform circular motion onto one of the axes in the x-y plane.

Learning Objectives

Depict relationship between the simple harmonic motion and compatible circular motion

Key Takeaways

Key Points

• Uniform round motion describes the motion of an object traveling a round path with constant speed. The one-dimensional projection of this movement can be described as elementary harmonic motion.
• In uniform circular motion, the velocity vector five is always tangent to the round path and constant in magnitude. The acceleration is constant in magnitude and points to the eye of the round path, perpendicular to the velocity vector at every instant.
• If an object moves with angular velocity ω around a circle of radius r centered at the origin of the x-y airplane, then its motion forth each coordinate is simple harmonic motion with aamplitude r and angular frequency ω.

Fundamental Terms

• centripetal acceleration: Dispatch that makes a torso follow a curved path: it is e'er perpendicular to the velocity of a trunk and directed towards the center of curvature of the path.
• uniform circular motility: Movement effectually a circular path with constant speed.

Compatible Circular Motion

Compatible circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the torso from the center of the circle remains constant at all times. Though the body's speed is abiding, its velocity is not constant: velocity (a vector quantity) depends on both the body's speed and its direction of travel. Since the torso is constantly changing management as it travels effectually the circle, the velocity is changing also. This varying velocity indicates the presence of an acceleration called the centripetal dispatch. Centripetal acceleration is of constant magnitude and directed at all times towards the center of the circle. This acceleration is, in plough, produced by a centripetal strength —a force in constant magnitude, and directed towards the center.

Velocity

The above figure illustrates velocity and acceleration vectors for compatible motion at four unlike points in the orbit. Since velocity 5 is tangent to the circular path, no two velocities signal in the aforementioned management. Although the object has a abiding speed, its direction is ever changing. This change in velocity is due to an dispatch, a, whose magnitude is (like that of the velocity) held constant, simply whose direction also is always changing. The acceleration points radially in (centripetally) and is perpendicular to the velocity. This acceleration is known equally centripetal dispatch.

Uniform Circular Motility (at Four Different Point in the Orbit): Velocity v and acceleration a in uniform circular motion at angular rate ω; the speed is constant, but the velocity is always tangent to the orbit; the acceleration has constant magnitude, but ever points toward the center of rotation

Displacement effectually a circular path is often given in terms of an bending θ. This bending is the angle between a directly line drawn from the heart of the circle to the objects starting position on the border and a directly line drawn from the objects ending position on the edge to heart of the circle. See for a visual representation of the bending where the point p started on the x- centrality and moved to its nowadays position. The angle θ describes how far it moved.

Project of Uniform Circular Motion: A point P moving on a circular path with a constant athwart velocity ω is undergoing uniform circular motility. Its project on the ten-centrality undergoes simple harmonic motion. Also shown is the velocity of this indicate around the circle, v−max, and its projection, which is v. Annotation that these velocities grade a like triangle to the displacement triangle.

For a path effectually a circumvolve of radius r, when an bending θ (measured in radians ) is swept out, the distance traveled on the border of the circle is s = rθ. You lot can bear witness this yourself by remembering that the circumference of a circle is 2*pi*r, so if the object traveled around the whole circle (ane circumference) it will take gone through an angle of 2pi radians and traveled a distance of 2pi*r. Therefore, the speed of travel around the orbit is:

[latex]\text{5}=\text{r}\frac{\text{d}\theta }{\text{dt}}=\text{r}\omega[/latex],

where the angular rate of rotation is ω. (Note that ω = 5/r. ) Thus, 5 is a constant, and the velocity vector 5 also rotates with constant magnitude v, at the aforementioned athwart rate ω.

Acceleration

The dispatch in uniform circular motion is always directed inwards and is given by:

[latex]\text{a}=\text{5}\frac{\text{d}\theta }{\text{dt}}=\text{v}\omega =\frac{\text{five}^{ii}}{\text{r}}[/latex].

This dispatch acts to change the direction of v, simply non the speed.

Uncomplicated Harmonic Motion from Uniform Circular Motion

There is an easy way to produce simple harmonic movement by using uniform circular motion. The figure below demonstrates one way of using this method. A ball is attached to a uniformly rotating vertical turntable, and its shadow is projected onto the floor as shown. The shadow undergoes uncomplicated harmonic motion.

Shadow of a Brawl Undergoing Simple Harmonic Motion: The shadow of a ball rotating at constant angular velocity ω on a turntable goes back and forth in precise simple harmonic movement.

The next figure shows the basic relationship between uniform round motion and uncomplicated harmonic motion. The point P travels around the circumvolve at constant angular velocity ω. The point P is analogous to the brawl on a turntable in the figure above. The project of the position of P onto a fixed axis undergoes simple harmonic motion and is analogous to the shadow of the object. At a signal in time assumed in the effigy, the projection has position x and moves to the left with velocity v. The velocity of the point P around the circle equals |five_max|. The project of |v_max| on the ten-axis is the velocity 5 of the uncomplicated harmonic motion along the x-axis.

To see that the projection undergoes simple harmonic motion, note that its position x is given by:

[latex]\text{x}=\text{Xcos}\theta[/latex],

where θ=ωt, ω is the constant angular velocity, and X is the radius of the circular path. Thus,

[latex]\text{x}=\text{Xcos}\omega \text{t}[/latex].

The athwart velocity ω is in radians per unit of measurement time; in this case 2π radians is the time for i revolution T. That is, ω=2π/T. Substituting this expression for ω, we see that the position ten is given past:

[latex]\text{x}(\text{t})=\text{cos}(\frac{2\pi \text{t}}{\text{T}})=\text{cos}(2\pi \text{ft})[/latex].

Annotation: This equation should look familiar from our earlier discussion of simple harmonic motion.

The Simple Pendulum

A elementary pendulum acts similar a harmonic oscillator with a period dependent simply on L and g for sufficiently small amplitudes.

Learning Objectives

Identify parameters that affect the period of a simple pendulum

Key Takeaways

Cardinal Points

• A simple pendulum is defined as an object that has a small mass, as well known every bit the pendulum bob, which is suspended from a wire or string of negligible mass.
• When displaced, a pendulum will oscillate effectually its equilibrium point due to momentum in balance with the restoring forcefulness of gravity.
• When the swings ( amplitudes ) are small, less than nearly 15º, the pendulum acts equally a simple harmonic oscillator with period [latex]\text{T}=2\pi \sqrt{\frac{\text{L}}{\text{g}}}[/latex], where L is the length of the string and g is the dispatch due to gravity.

Key Terms

• uncomplicated pendulum: A hypothetical pendulum consisting of a weight suspended past a weightless string.

The Simple Pendulum

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting equilibrium position, it is discipline to a restoring force; after it reaches its highest point in its swing, gravity volition accelerate it back toward the equilibrium position. When released, the restoring forcefulness combined with the pendulum's mass causes information technology to oscillate well-nigh the equilibrium position, swinging back and forth.

Unproblematic Pendulum: A uncomplicated pendulum has a modest-diameter bob and a string that has a very small mass but is stiff enough non to stretch appreciably. The linear displacement from equilibrium is due south, the length of the arc. Likewise shown are the forces on the bob, which result in a net forcefulness of −mgsinθ toward the equilibrium position—that is, a restoring force.

For small displacements, a pendulum is a elementary harmonic oscillator. A simple pendulum is defined to take an object that has a small mass, also known as the pendulum bob, which is suspended from a wire or string of negligible mass, such as shown in the illustrating figure. Exploring the uncomplicated pendulum a bit farther, we tin can find the conditions under which it performs simple harmonic motion, and nosotros tin derive an interesting expression for its menstruation.

Pendulums: A brief introduction to pendulums (both platonic and concrete) for calculus-based physics students from the standpoint of elementary harmonic motion.

We begin past defining the displacement to exist the arc length due south. We see from the figure that the net force on the bob is tangent to the arc and equals −mgsinθ. (The weight mg has components mgcosθ along the string and mgsinθ tangent to the arc. ) Tension in the string exactly cancels the component mgcosθ parallel to the string. This leaves a net restoring forcefulness drawing the pendulum back toward the equilibrium position at θ = 0.

Now, if we can prove that the restoring force is directly proportional to the displacement, so we have a unproblematic harmonic oscillator. In trying to determine if we have a simple harmonic oscillator, we should note that for pocket-size angles (less than about 15º), sinθ≈θ (sinθ and θ differ by most 1% or less at smaller angles). Thus, for angles less than nearly 15º, the restoring force F is

[latex]\text{F}\approx -\text{mg}\theta[/latex].

The deportation s is directly proportional to θ. When θ is expressed in radians, the arc length in a circumvolve is related to its radius (Fifty in this instance) by:

[latex]\text{s}=\text{L}\theta[/latex]

and so that

[latex]\theta=\frac{\text{due south}}{\text{L}}[/latex].

For small angles, and so, the expression for the restoring forcefulness is:

[latex]\text{F}\approx \frac{\text{mgL}}{\text{s}}[/latex].

This expression is of the form of Hooke's Police force:

[latex]\text{F}\approx -\text{kx}[/latex]

where the force constant is given by thousand=mg/L and the displacement is given by 10=s. For angles less than about 15º, the restoring force is directly proportional to the displacement, and the simple pendulum is a elementary harmonic oscillator.

Using this equation, we can detect the menstruum of a pendulum for amplitudes less than nearly 15º. For the simple pendulum:

[latex]\text{T}=2\pi \sqrt{\frac{\text{g}}{\text{g}}}=ii\pi\sqrt{\frac{\text{m}}{\frac{\text{mg}}{\text{L}}}}[/latex].

Thus,

[latex]\text{T}=ii\pi \sqrt{\frac{\text{L}}{\text{m}}}[/latex]

or the menses of a simple pendulum. This upshot is interesting because of its simplicity. The only things that affect the period of a simple pendulum are its length and the acceleration due to gravity. The period is completely independent of other factors, such as mass. Even simple pendulum clocks can be finely adjusted and accurate. Notation the dependence of T on grand. If the length of a pendulum is precisely known, information technology can actually exist used to mensurate the acceleration due to gravity. If θ is less than nigh 15º, the catamenia T for a pendulum is nearly contained of amplitude, equally with simple harmonic oscillators. In this case, the motion of a pendulum every bit a function of fourth dimension can be modeled as:

[latex]\theta (\text{t})=\theta _{\text{o}}\text{cos}(\frac{2\pi \text{t}}{\text{T}})[/latex]

For amplitudes larger than 15º, the period increases gradually with aamplitude so it is longer than given past the simple equation for T above. For instance, at an amplitude of θ₀ = 23° it is 1% larger. The period increases asymptotically (to infinity) as θ₀ approaches 180°, because the value θ₀ = 180° is an unstable equilibrium point for the pendulum.

The Physical Pendulum

The menses of a concrete pendulum depends upon its moment of inertia nearly its pin point and the distance from its center of mass.

Learning Objectives

Identify parameters that affect the menstruation of a physical pendulum

Key Takeaways

Key Points

• A concrete pendulum is the generalized example of the simple pendulum. It consists of whatever rigid body that oscillates about a pin point.
• For small amplitudes, the flow of a physical pendulum merely depends on the moment of inertia of the body around the pivot indicate and the distance from the pivot to the body'due south center of mass. Information technology is calculated as: [latex]\text{T}=two\pi \sqrt{\frac{\text{I}}{\text{mgh}}}[/latex].
• The period is still independent of the full mass of the rigid body. However, it is not independent of the mass distribution of the rigid body. A change in shape, size, or mass distribution volition change the moment of inertia and thus, the catamenia.

Key Terms

• concrete pendulum: A pendulum where the rod or cord is not massless, and may have extended size; that is, an arbitrarily-shaped, rigid body swinging past a pivot. In this case, the pendulum'southward period depends on its moment of inertia around the pivot point.
• mass distribution: Describes the spatial distribution, and defines the middle, of mass in an object.

The Physical Pendulum

Think that a simple pendulum consists of a mass suspended from a massless cord or rod on a frictionless pivot. In that case, we are able to fail whatsoever result from the string or rod itself. In contrast, a physical pendulum (sometimes called a compound pendulum) may exist suspended by a rod that is not massless or, more than mostly, may exist an arbitrarily-shaped, rigid body swinging by a pivot (see ). In this instance, the pendulum's period depends on its moment of inertia effectually the pivot point.

Pendulums – Physical Pendulum: A brief introduction to pendulums (both ideal and physical) for calculus-based physics students from the standpoint of simple harmonic motion.

A Physical Pendulum: An instance showing how forces deed through eye of mass. Nosotros tin can calculate the period of this pendulum by determining the moment of inertia of the object effectually the pivot point.

Gravity acts through the middle of mass of the rigid body. Hence, the length of the pendulum used in equations is equal to the linear distance between the pivot and the middle of mass (h).

The equation of torque gives:

[latex]\tau=\text{I}\alpha[/latex],

where α is the athwart acceleration, τ is the torque, and I is the moment of inertia.

The torque is generated by gravity then:

[latex]\tau=\text{mghsin}\theta[/latex],

where h is the distance from the eye of mass to the pivot point and θ is the angle from the vertical.

Hence, under the small-angle approximation sin\theta \approx \theta,

[latex]\alpha\approx -\frac{\text{mgh}\theta }{\text{I}}[/latex].

This is of the same form every bit the conventional unproblematic pendulum and this gives a flow of:

[latex]\text{T}=2\pi \sqrt{\frac{\text{I}}{\text{mgh}}}[/latex].

And a frequency of:

[latex]\text{f}=\frac{i}{\text{T}}=\frac{one}{2\pi }\sqrt{\frac{\text{mgh}}{\text{I}}}[/latex].

In case we know the moment of inertia of the rigid trunk, we can evaluate the above expression of the menstruation for the physical pendulum. For illustration, let u.s. consider a compatible rigid rod, pivoted from a frame equally shown (come across ). Conspicuously, the middle of mass is at a distance L/two from the point of suspension:

Uniform Rigid Rod: A rigid rod with uniform mass distribution hangs from a pivot point. This is another example of a concrete pendulum.

[latex]\text{h}=\frac{\text{L}}{ii}[/latex].

The moment of inertia of the rigid rod about its centre is:

[latex]\text{I}_{\text{c}}=\frac{\text{mL}^{2}}{12}[/latex].

However, nosotros need to evaluate the moment of inertia about the pin point, not the center of mass, so we apply the parallel axis theorem:

[latex]\text{I}_{\text{o}}=\text{I}_{\text{c}}+\text{mh}^{2}=\frac{\text{mL}^{ii}}{12}+\text{m}(\frac{\text{50}}{two})^{2}=\frac{\text{mL}^{2}}{three}[/latex].

Plugging this consequence into the equation for period, we take:

[latex]\text{T}=2\pi \sqrt{\frac{\text{I}}{\text{mgh}}}=2\pi\sqrt{\frac{2\text{mL}^{2}}{three\text{mgL}}}=2\pi\sqrt{\frac{2\text{L}}{three\text{g}}}[/latex].

The of import matter to notation about this relation is that the period is still contained of the mass of the rigid body. Still, it is non independent of the mass distribution of the rigid body. A change in shape, size, or mass distribution will change the moment of inertia. This, in turn, volition change the menses.

As with a simple pendulum, a physical pendulum can be used to measure out g.

Energy in a Unproblematic Harmonic Oscillator

The total energy in a elementary harmonic oscillator is the constant sum of the potential and kinetic energies.

Learning Objectives

Explain why the total free energy of the harmonic oscillator is abiding

Primal Takeaways

Key Points

• The sum of the kinetic and potential energies in a simple harmonic oscillator is a constant, i.due east., KE+PE=constant. The energy oscillates back and forth betwixt kinetic and potential, going completely from one to the other as the arrangement oscillates.
• In a spring arrangement, the conservation equation is written every bit: [latex]\frac{1}{ii}\text{mv}^{2}+\frac{1}{2}\text{kx}^{2}=constant=\frac{1}{two}\text{kX}^{2}[/latex], where X is the maximum deportation.
• The maximum velocity depends on three factors: amplitude, the stiffness factor, and mass: [latex]\text{v}_{\text{max}}=\sqrt{\frac{\text{k}}{\text{m}}}\text{X}[/latex].

Cardinal Terms

• rubberband potential energy: The energy stored in a deformable object, such every bit a spring.
• dissipative forces: Forces that cause free energy to exist lost in a system undergoing motility.

Energy in a Elementary Harmonic Oscillator

To report the energy of a elementary harmonic oscillator, we first consider all the forms of energy it tin can take. Recall that the potential energy (PE), stored in a bound that follows Hooke'south Law is:

[latex]\text{PE}=\frac{1}{ii}\text{kx}^{2}[/latex],

where PE is the potential energy, one thousand is the spring abiding, and ten is the magnitude of the displacement or deformation. Because a simple harmonic oscillator has no dissipative forces , the other important course of energy is kinetic energy (KE). Conservation of free energy for these two forms is:

[latex]\text{KE}+\text{PE}=\text{constant}[/latex],

which can be written as:

[latex]\frac{ane}{two}\text{mv}^{2}+\frac{1}{2}\text{kx}^{ii}=\text{constant}[/latex].

This statement of conservation of energy is valid for all simple harmonic oscillators, including ones where the gravitational force plays a part. For example, for a simple pendulum we replace the velocity with v=Lω, the spring constant with thousand=mg/L, and the displacement term with x=Lθ. Thus:

[latex]\frac{1}{2}\text{mL}^{ii}\omega ^{2}+\frac{1}{two}\text{mgL}\theta ^{2}=\text{constant}[/latex].

In the example of undamped, simple harmonic motion, the energy oscillates dorsum and forth between kinetic and potential, going completely from one to the other as the organization oscillates. So for the simple instance of an object on a frictionless surface attached to a leap, every bit shown again (see ), the motility starts with all of the energy stored in the spring. Every bit the object starts to move, the rubberband potential energy is converted to kinetic energy, becoming entirely kinetic energy at the equilibrium position. It is so converted back into elastic potential energy by the leap, the velocity becomes zippo when the kinetic free energy is completely converted, and so on. This concept provides extra insight here and in later applications of uncomplicated harmonic motion, such equally alternating current circuits.

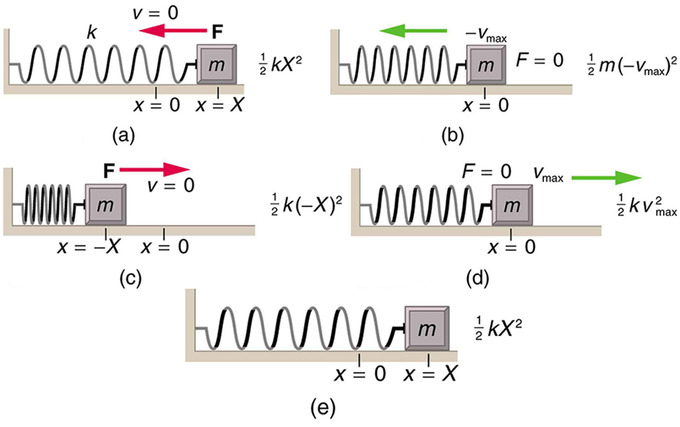
Energy in a Simple Harmonic Oscillator: The transformation of energy in elementary harmonic move is illustrated for an object attached to a spring on a frictionless surface. (a) The mass has achieved maximum deportation from equilibrium. All free energy is potential energy. (b) As the mass passes through the equilibrium point with maximum speed all energy in the system is in kinetic energy. (c) Once once more, all free energy is in the potential course, stored in the pinch of the spring (in the get-go panel the energy was stored in the extension of the spring). (d) Passing through equilibrium over again all energy is kinetic. (e) The mass has completed an entire bike.

The conservation of free energy principle tin can be used to derive an expression for velocity v. If nosotros start our simple harmonic motion with zero velocity and maximum displacement (x=X), then the total energy is:

[latex]\text{Eastward}=\frac{i}{2}\text{kX}^{2}[/latex].

This total energy is constant and is shifted back and along between kinetic free energy and potential free energy, at most times being shared by each. The conservation of energy for this arrangement in equation class is thus:

[latex]\frac{ane}{2}\text{mv}^{2}+\frac{i}{2}\text{kx}^{ii}=\frac{ane}{2}\text{kX}^{two}[/latex].

Solving this equation for v yields:

[latex]\text{v}=\pm \sqrt{\frac{\text{grand}}{\text{k}}(\text{X}^{2}-\text{x}^{2})}[/latex].

Manipulating this expression algebraically gives:

[latex]\text{5}=\pm \sqrt{\frac{\text{k}}{\text{m}}}\text{X}\sqrt{1-\frac{\text{ten}^{2}}{\text{Ten}^{two}}}[/latex],

and so:

[latex]\text{v}=\pm \text{v}_{\text{max}}\sqrt{ane-\frac{\text{x}^{two}}{\text{X}^{2}}}[/latex],

where:

[latex]\text{v}_{\text{max}}=\sqrt{\frac{\text{grand}}{\text{thou}}}\text{10}[/latex].

From this expression, we run across that the velocity is a maximum (v_max) at 10=0. Notice that the maximum velocity depends on three factors. It is directly proportional to amplitude. As you might guess, the greater the maximum displacement, the greater the maximum velocity. Information technology is as well greater for stiffer systems because they exert greater forcefulness for the same displacement. This observation is seen in the expression for 5_max; it is proportional to the square root of the force constant k. Finally, the maximum velocity is smaller for objects that take larger masses, because the maximum velocity is inversely proportional to the square root of m. For a given force, objects that take large masses advance more slowly.

A similar calculation for the simple pendulum produces a like result, namely:

[latex]\omega_{\text{max}}=\sqrt{\frac{\text{k}}{\text{Fifty}}}\theta _{\text{max}}[/latex].

Experience with a simple harmonic oscillator: A known mass is hung from a bound of known spring constant and allowed to oscillate. The time for one oscillation (menses) is measured. This value is compared to a predicted value, based on the mass and leap abiding.

Sinusoidal Nature of Simple Harmonic Movement

The solutions to the equations of motion of unproblematic harmonic oscillators are ever sinusoidal, i.east., sines and cosines.

Learning Objectives

Review factors responsible for the sinusoidal behavior of uniform circular movement

Primal Takeaways

Key Points

• For elementary harmonic oscillators, the equation of motion is always a second order differential equation that relates the acceleration and the displacement. The relevant variables are x, the displacement, and k, the leap abiding.
• Solving the differential equation above always produces solutions that are sinusoidal in nature. For example, x(t), v(t), a(t), 1000(t), and U(t) all take sinusoidal solutions for elementary harmonic movement.
• Uniform circular motion is as well sinusoidal because the projection of this motion behaves like a simple harmonic oscillator.

Key Terms

• sinusoidal: In the form of a wave, specially one whose amplitude varies in proportion to the sine of some variable (such equally time).

Sinusoidal Nature of Simple Harmonic Motion

Why are sine waves so mutual?

If the mass -on-a-jump system discussed in previous sections were to exist constructed and its motility were measured accurately, its x–t graph would exist a near-perfect sine-moving ridge shape, as shown in. It is called a "sine wave" or "sinusoidal" even if it is a cosine, or a sine or cosine shifted by some arbitrary horizontal amount. Information technology may non exist surprising that it is a wiggle of this full general sort, but why is information technology a specific mathematically perfect shape? Why is it not a sawtooth shape, like in (2); or some other shape, like in (3)? It is notable that a vast number of apparently unrelated vibrating systems prove the same mathematical characteristic. A tuning fork, a sapling pulled to 1 side and released, a car bouncing on its shock absorbers, all these systems will exhibit sine-moving ridge movement under one condition: the amplitude of the move must be small-scale.

Sinusoidal and Non-Sinusoidal Vibrations: Just the elevation graph is sinusoidal. The others vary with constant aamplitude and flow, but do no depict simple harmonic motion.

Hooke'south Police force and Sine Moving ridge Generation

The primal to understanding how an object vibrates is to know how the force on the object depends on the object's position. If a system follows Hooke'due south Law, the restoring force is proportional to the displacement. As touched on in previous sections, at that place exists a second order differential equation that relates acceleration and displacement.

[latex]\text{F}_{\text{cyberspace}}=\text{grand}\frac{\text{d}^{2}\text{ten}}{\text{dt}^{2}}=-\text{kx}[/latex].

When this general equation is solved for the position, velocity and dispatch every bit a function of time:

• [latex]\text{10}(\text{t})=\text{Acos}(\omega \text{t}-\varphi )[/latex]
• [latex]\text{5}(\text{t})=\frac{\text{dx}}{\text{dt}}=-\text{A}\omega \text{sin}(\omega \text{t}-\varphi )[/latex]
• [latex]\text{a}(\text{t})=\frac{\text{d}^{2}\text{x}}{\text{dt}^{2}}=-\text{A}\omega^{2} \text{cos}(\omega \text{t}-\varphi )[/latex]

These are all sinusoidal solutions. Consider a mass on a bound that has a pocket-sized pen within running across a moving strip of newspaper as information technology bounces, recording its movements.

Mass on Jump Producing Sine Moving ridge: The vertical position of an object bouncing on a spring is recorded on a strip of moving paper, leaving a sine wave.

The in a higher place equations can be rewritten in a form applicative to the variables for the mass on jump system in the effigy.

• [latex]\text{x}(\text{t})=\text{Xcos}(\frac{two\pi \text{t}}{\text{T}})[/latex]
• [latex]\text{v}(\text{t})=-\text{five}_{\text{max}}\text{sin}(\frac{2\pi \text{t}}{\text{T}})[/latex]
• [latex]\text{a}(\text{t})=-\frac{\text{kX}}{\text{k}}\text{cos}(\frac{2\pi \text{t}}{\text{T}})[/latex]

Recall that the projection of uniform circular motion can be described in terms of a unproblematic harmonic oscillator. Uniform circular motion is therefore also sinusoidal, every bit you tin meet from.

Sinusoidal Nature of Compatible Circular Motion: The position of the projection of uniform round movement performs uncomplicated harmonic motion, as this wavelike graph of x versus t indicates.

Instantaneous Energy of Simple Harmonic Motion

The equations discussed for the components of the full energy of unproblematic harmonic oscillators may be combined with the sinusoidal solutions for x(t), v(t), and a(t) to model the changes in kinetic and potential energy in elementary harmonic motion.

The kinetic energy K of the system at time t is:

[latex]\text{Thousand}(\text{t})=\frac{1}{2}\text{mv}^{2}(\text{t})=\frac{1}{two}\text{thousand}\omega ^{ii}\text{A}^{2}\text{sin}^{two}(\omega \text{t}-\varphi )=\frac{one}{2}\text{kA}^{ii}\text{sin}^{2}(\omega \text{t}-\varphi )[/latex].

The potential energy U is:

[latex]\text{U}(\text{t})=\frac{1}{2}\text{kx}^{2}(\text{t})==\frac{ane}{two}\text{kA}^{2}\text{cos}^{2}(\omega \text{t}-\varphi )[/latex].

Summing K(t) and U(t) produces the full mechanical free energy seen earlier:

[latex]\text{Eastward}=\text{Thou}+\text{U}=\frac{1}{2}\text{kA}^{2}[/latex].

Source: https://courses.lumenlearning.com/boundless-physics/chapter/periodic-motion/

Posted by: acostaablee1955.blogspot.com

Share this post